[CS50] 알고리즘

업데이트: June 20, 2021

검색 알고리즘

배열은 한 자료형의 여러 값들이 메모리상에 모여 있는 구조이다.
컴퓨터는 이 값들에 접근할 때 배열의 인덱스 하나하나를 접근한다.

선형 검색

배열의 인덱스를 처음부터 끝까지 하나씩 증가시키면서 방문하여 그 값이 속하는지를 검사한다.
의사코드

For i from 0 to n–1
    If i'th element is 50
        Return true
Return false

이진 검색

배열이 정렬되어 있다면, 배열 중간 인덱스부터 시작하여 찾고자 하는 값과 비교하며 그보다 작은(작은 값이 저장되어 있는) 인덱스 또는 큰(큰 값이 저장되어 있는) 인덱스로 이동을 반복하면 된다.
의사코드

If no items
    Return false

If middle item is 50
    Return true

Else if 50 < middle item
    Search left half

Else if 50 > middle item
    Search right half

알고리즘 표기법

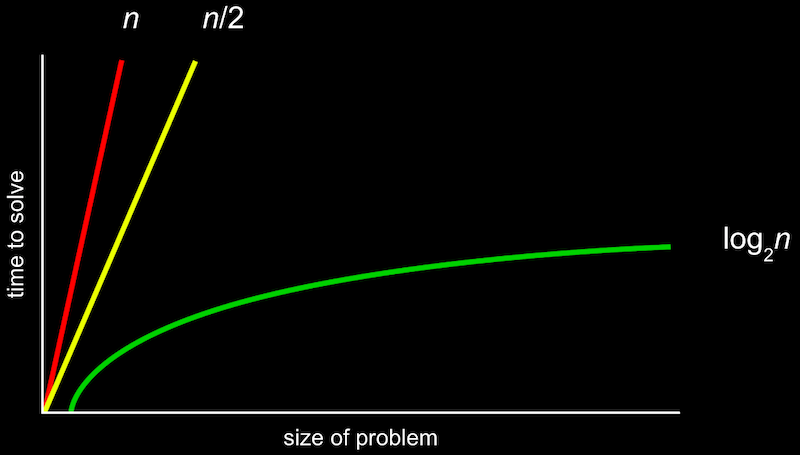
알고리즘시간

위와 같은 그림을 공식으로 표기한 것이 Big O 표기법이다.
O는 “on the order of”의 약자로, 쉽게 생각하면 ~만큼의 정도로 커지는 것이라고 볼 수 있다.
O(n)은 n만큼 커지는 것이므로 n이 늘어날수록 선형적으로 증가하게 된다.
O(n/2)도 결국 n이 매우 커지면 1/2은 큰 의미가 없어지므로 O(n)이라고 볼 수 있다.
주로 아래 목록과 같은 Big O 표기가 실행 시간을 나타내기 위해 많이 사용된다.
- O(n^2)
- O(n log n)
- O(n) - 선형 검색
- O(log n) - 이진 검색
- O(1)

Big O가 알고리즘 실행 시간의 상한을 나타낸 것이라면, 반대로 Big Ω는 알고리즘 실행 시간의 하한을 나타낸다.
예를 들어 선형 검색에서는 n개의 항목이 있을 때 최대 n번의 검색을 해야 하므로 상한이 O(n)이 되지만 운이 좋다면 한 번만에 검색을 끝낼수도 있으므로 하한은 Ω(1)이 된다.
Big Ω 표기 종류
- Ω(n^2)
- Ω(n log n)
- Ω(n) - 배열 안에 존재하는 값의 개수 세기
- Ω(log n)
- Ω(1) - 선형 검색, 이진 검색

선형 검색

찾고자 하는 자료를 검색하는 데 사용되는 알고리즘 중 하나
선형 검색은 원하는 원소가 발견될 때까지 처음부터 마지막 자료까지 차례대로 검색한다.

효율성 그리고 비효율성

선형 검색 알고리즘은 정확하지만 아주 효율적이지 못한 방법이다.
리스트의 길이가 n이라고 했을 때, 최악의 경우 리스트의 모든 원소를 확인해야 하므로 n번만큼 실행된다.
반대로 최선의 상황은 처음 시도했을 때 찾고자 하는 값이 있는 경우
평균적으로 선형 검색이 최악의 상황에서 종료되는 것에 가깝다고 가정할 수 있다.
선형 검색은 자료가 정렬되어 있지 않거나 그 어떤 정보도 없이 하나씩 찾아야 하는 경우에 유용하다.
정렬은 시간이 오래 걸리고 공간을 더 차지한다.
하지만 이 추가적인 과정을 진행하면 여러 번 리스트를 검색해야 하거나 매우 큰 리스트를 검색해야 할 경우 시간을 단축할 수 있을 것이다.

#include <cs50.h>
#include <stdio.h>

int main(void)
{
    // numbers 배열 정의 및 값 입력
    int numbers[] = {4, 8, 15, 16, 23, 42};

    // 값 50 검색
    for (int i = 0; i < 6; i++)
    {
        if (numbers[i] == 50)
        {
            printf("Found\n");
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

주어진 배열에서 특정 값을 찾기 위해 선형 검색을 사용한 코드이다.
배열의 크기만큼 for 루프를 돌면서 배열의 인덱스를 차례대로 방문하며 찾는 값이 있는지를 검사한다.

문자열로 이루어진 배열도 비슷한 방식으로 검색할 수 있다.

#include <cs50.h>
#include <stdio.h>
#include <string.h>

int main(void)
{
    string names[] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"};
    string numbers[] = {"617–555–0100", "617–555–0101", "617–555–0102", "617–555–0103"};

    for (int i = 0; i < 4; i++)
    {
        if (strcmp(names[i], "EMMA") == 0)
        {
            printf("Found %s\n", numbers[i]);
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

names 배열과 numbers 배열을 따로 정의하고 names 배열에서 검색해서 해당하는 인덱스의 numbers 배열 값을 출력한다.
이 경우에는 names 배열과 numbers 배열이 서로 같은 인덱스를 가져야 한다는 한계가 있다.

#include <cs50.h>
#include <stdio.h>
#include <string.h>

typedef struct
{
    string name;
    string number;
}
person;

int main(void)
{
    person people[4];

    people[0].name = "EMMA";
    people[0].number = "617–555–0100";
    people[1].name = "RODRIGO";
    people[1].number = "617–555–0101";
    people[2].name = "BRIAN";
    people[2].number = "617–555–0102";
    people[3].name = "DAVID";
    people[3].number = "617–555–0103";

    // EMMA 검색
    for (int i = 0; i < 4; i++)
    {
        if (strcmp(people[i].name, "EMMA") == 0)
        {
            printf("Found %s\n", people[i].number);
            return 0;
        }
    }
    printf("Not found\n");
    return 1;
}

더 좋은 방법은 위의 코드와 같이 새로운 자료형으로 구조체를 정의해서 이름과 번호를 묶어주는 것이다.
person이라는 이름의 구조체를 자료형으로 정의하고 person 자료형의 배열을 선언하면 그 안에 포함된 속성값은 ‘.’으로 연결해서 접근할 수 있다.
person a; 라는 변수가 있다면, a.name 또는 a.number 이 각각 이름과 전화번호를 저장하는 변수가 된다. 이렇게 함으로써 더욱 확장성 있는 전화번호부 검색 프로그램을 만들 수 있다.

버블 정렬

버블 정렬은 두 개의 인접한 자료 값을 비교하면서 위치를 교환하는 방식으로 정렬하는 방법을 말한다.
단 두 개의 요소만 정렬해주는 좁은 범위의 정렬에 집중한다.
접근법은 간단하지만 단 하나의 요소를 정렬하기 위해 너무 많이 교환하는 낭비가 발생할 수도 있다.

아래 숫자들을 오름차순으로 정렬하기 위한 과정
6 3 8 5 2 7 4 1
- 교환 전: 6 3 8 5 2 7 4 1
- 교환 후: 3 6 8 5 2 7 4 1
- 교환 전: 3 6 8 5 2 7 4 1
- 교환 후: 3 6 5 8 2 7 4 1
- 끝까지 반복 : 3 6 5 2 7 4 1 8
아직 오름차순으로 정렬이 되지 않았기 때문에 다시 처음부터 동일한 작업을 반복한다.
- 3 6 5 2 7 4 1 8
- 3 6 5 2 7 4 1 8 (교환)
- 3 5 6 2 7 4 1 8 (교환)
- 3 5 2 6 7 4 1 8
- 3 5 2 6 7 4 1 8 (교환)
- 3 5 2 6 4 7 1 8 (교환)
- 3 5 2 6 4 1 7 8
이 과정을 끝까지 반복하면 최종적으로 아래와 같이 오름차순 정렬이 된다.
- 1 2 4 3 5 6 7 8
이러한 정렬 방식을 버블 정렬이라 한다.
마치 거품이(비교 및 교환이) 터지면서 위로 올라오는 (배열의 옆으로 이동하는) 방식이기 때문이다.
의사코드

Repeat n–1 times

    For i from 0 to n–2

        If i'th and i+1'th elements out of order

            Swap them

중첩 루프를 돌아야 하고, n개의 값이 주어졌을 때 각 루프는 각각 n-1번, n-2번 반복되므로 (n−1)∗(n−2)=n₂−3n+2번의 비교 및 교환이 필요하다.
여기서 가장 크기가 큰 요소는 n^2 이므로 위와 같은 코드로 작성한 버블 정렬 실행 시간의 상한은 O(n^2)라고 말할 수 있다.
정렬이 되어 있는지 여부에 관계 없이 루프를 돌며 비교를 해야 하므로 위와 같은 코드로 작성한 버블 정렬의 실행 시간의 하한도 여전이 Ω(n^2)이 된다.

선택 정렬

선택 정렬은 배열 안의 자료 중 가장 작은 수(혹은 가장 큰 수)를 찾아 첫 번째 위치(혹은 가장 마지막 위치)의 수와 교환해주는 방식의 정렬이다.
선택 정렬은 교환 횟수를 최소화하는 반면 각 자료를 비교하는 횟수는 증가한다.

오름차순 정렬 과정
6 3 8 5 2 7 4 1
먼저 숫자들 중 가장 작은 값을 찾는다.
- 6 3 8 5 2 7 4 1
가장 작은 값인 1은 가장 앞에 있어야 하므로 현재 리스트의 첫 번째 값인 6과 교환한다.
- 1 3 8 5 2 7 4 6
1은 제외하고, 두 번째 숫자부터 또 가장 작은 값을 찾는다.
- 1 3 8 5 2 7 4 6
2는 정렬되지 않는 숫자들 중에서 가장 앞에 있어야 하므로 3과 교환한다.
- 1 2 8 5 3 7 4 6
이 과정을 더 이상 교환이 일어나지 않을때까지 반복하면 정렬이 완료된다.
- 1 2 3 4 5 6 7 8

의사코드

For i from 0 to n–1

    Find smallest item between i'th item and last item

    Swap smallest item with i'th item

여기서도 두 번의 루프를 돌아야 한다.
바깥 루프에서는 숫자들을 처음부터 순서대로 방문하고, 안쪽 루프에서는 가장 작은 값을 찾는다.
소요 시간의 상한은 O(n^2)이 된다. 하한도 마찬가지로 Ω(n^2)이다. 버블 정렬과 동일하다.

정렬 알고리즘의 실행시간

여태까지 배운 선형 검색, 이진 검색, 버블 정렬, 선택 정렬의 실행시간은 각각 어떻게 되는지 정리해보자.

실행시간의 상한

O(n^2) : 선택 정렬, 버블 정렬
O(n log n)
O(n) : 선형 검색
O(log n) : 이진 검색
O(1)

실행시간의 하한

Ω(n^2): 선택 정렬, 버블 정렬
Ω(n log n)
Ω(n)
Ω(log n)
Ω(1): 선형 검색, 이진 검색

여기서 버블 정렬을 좀 더 잘할 수 있는 방법
만약 정렬이 모두 되어 있는 숫자 리스트가 주어진다면 어떨까?
원래의 의사코드

Repeat n–1 times

    For i from 0 to n–2

        If i'th and i+1'th elements out of order

            Swap them

여기서 안쪽 루프에서 만약 교환이 하나도 일어나지 않는다면 이미 정렬이 잘 되어 있는 상황
따라서 바깥쪽 루프를 ‘교환이 일어나지 않을때’까지만 수행하도록 다음과 같이 바꿀 수 있다.

Repeat until no swaps

    For i from 0 to n–2

        If i'th and i+1'th elements out of order

            Swap them

따라서 최종적으로 버블 정렬의 하한은 Ω(n)이 된다. 상황에 따라서는 선택 정렬보다 더 빠른 방법이 된다.

실행시간의 하한

Ω(n^2): 선택 정렬
Ω(n log n)
Ω(n): 버블 정렬
Ω(log n)
Ω(1): 선형 검색, 이진 검색

재귀

함수가 본인 스스로를 호출해서 사용할 수 있는 것을 재귀라고 한다.
아래와 같이 피라미드 모양을 출력하기 위해 다음과 같은 코드를 작성할 수 있다.

#
##
###
####

#include <cs50.h>
#include <stdio.h>

void draw(int h);

int main(void)
{
    // 사용자로부터 피라미드의 높이를 입력 받아 저장
    int height = get_int("Height: ");

    // 피라미드 그리기
    draw(height);
}

void draw(int h)
{
    // 높이가 h인 피라미드 그리기
    for (int i = 1; i <= h; i++)
    {
        for (int j = 1; j <= i; j++)
        {
            printf("#");
        }
        printf("\n");
    }
}

높이를 입력받아 중첩 루프를 이용해 피라미드를 출력해주는 draw 함수를 정의했다.
중첩 루프 없이 바깥 루프를 없앤 draw 함수를 만들고 이를 ‘재귀적’으로 호출하도록 해서 똑같은 작업을 수행할 수 있다.

#include <cs50.h>
#include <stdio.h>

void draw(int h);

int main(void)
{
    int height = get_int("Height: ");

    draw(height);
}

void draw(int h)
{
    // 높이가 0이라면 (그릴 필요가 없다면)
    if (h == 0)
    {
        return;
    }

    // 높이가 h-1인 피라미드 그리기
    draw(h - 1);

    // 피라미드에서 폭이 h인 한 층 그리기
    for (int i = 0; i < h; i++)
    {
        printf("#");
    }
    printf("\n");
}

h라는 높이를 받았을 때, h-1 높이로 draw 함수를 먼저 호출하고, 그 후에 h 만큼의 #을 출력한다. 여기서 내부적으로 호출된 draw 함수를 따라가다 보면 h = 0인 상황이 오게 된다.
따라서 그 때는 아무것도 출력하지 않도록 하는 조건문을 추가해야 한다.
이렇게 재귀를 이용하면 중첩루프를 사용하지 않고도 하나의 함수로 동일한 작업을 수행할 수 있다.

병합 정렬

분할 정복 탐색처럼 데이터를 반으로 나누어간다는 것과 공통점이 있는 방법인 병합 정렬(합병 정렬)이 있다.
병합 정렬은 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합쳐나가며 정렬을 하는 방식이다.
이 과정은 재귀적으로 구현되기 때문에 재귀를 학습하면 이해하기 더 쉽다.

아래 숫자들을 오름차순으로 정렬하는 과정
7 4 5 2 6 3 8 1
숫자를 반으로 나눈다.
- 7 4 5 2 6 3 8 1
나눠진 부분 중 첫 번째를 한번 더 반으로 나눈다.
- 7 4 5 2 6 3 8 1
마지막으로 한 번 더 나눈다.
- 7 4 5 2 6 3 8 1
숫자가 두 개 밖에 남지 않았으므로 더이상 나누지 않고, 두 숫자를 다시 병합한다.
이때 작은 숫자가 먼저 오도록 한다. 4와 7의 순서를 바꿔서 병합
- 4 7 5 2 6 3 8 1
마찬가지로 5 2 부분도 반으로 나눈 후 작은 숫자가 먼저 오도록 다시 병합한다.
- 4 7 2 5 6 3 8 1
4 7과 2 5 두 개의 부분을 병합한다. 각 부분의 숫자들을 앞에서부터 순서대로 읽어들여 비교하여 더 작은 숫자를 병합되는 부분에 가져온다.
즉, 4와 2를 먼저 비교해서 2를 가져온다. 그 후에 4와 5를 비교해서 4를 가져온다. 그리고 7과 5를 비교해서 5를 가져오고, 남은 7을 가져온다.
- 2 4 5 7 6 3 8 1
이제 남은 오른쪽 4개의 숫자도 위와 동일한 과정을 거친다.
- 2 4 5 7 1 3 6 8
마지막으로 각각 정렬된 왼쪽 4개와 오른쪽 4개의 두 부분을 병합한다. 2와 1을 비교하고, 1을 가져온다. 2와 3을 비교하고, 2를 가져온다. 4와 3을 비교하고, 3을 가져온다… 이 과정을 병합이 끝날때까지 진행하면 아래와 같이 정렬이 완료된다.
- 1 2 3 4 5 6 7 8

전체 과정을 요약해서 도식화해보면 아래와 같다.

1 → 가장 작은 부분 (숫자 1개)으로 나눠진 결과입니다.

4 7 2 5 3 6 1 8 → 숫자 1개씩을 정렬하여 병합한 결과입니다.
2 4 5 7 1 3 6 8 → 숫자 2개씩을 정렬하여 병합한 결과입니다.
1 2 3 4 5 6 7 8 → 마지막으로 숫자 4개씩을 정렬하여 병합한 결과입니다.

이러한 방법을 ‘병합 정렬’이라 한다.
병합 정렬 실행 시간의 상한은 O(n log n)이다.
숫자들을 반으로 나누는 데에는 O(log n)의 시간이 들고, 각 반으로 나눈 부분들을 다시 정렬해서 병합하는 데 각각 O(n)의 시간이 걸리기 때문이다.
실행 시간의 하한도 역시 Ω(n log n)이다. 숫자들이 이미 정렬되었는지 여부에 관계 없이 나누고 병합하는 과정이 필요하기 때문이다.

Twitter Google+ LinkedIn

techhan

[CS50] 알고리즘

검색 알고리즘

선형 검색

이진 검색

알고리즘 표기법

선형 검색

효율성 그리고 비효율성

버블 정렬

선택 정렬

정렬 알고리즘의 실행시간

실행시간의 상한

실행시간의 하한

실행시간의 하한

재귀

병합 정렬

공유하기

댓글남기기

관련 글 더보기

[정올] 1658_최대공약수와 최소공배수 (JAVA)

[정올] 2809_약수 (JAVA)

[정올] 1402_약수 구하기 (JAVA)

[정올] 1071_약수와 배수 (JAVA)